Binary Tree in C programming

Trees

A tree is a nonlinear, two-dimensional data structure with special properties. Tree nodes contain two or more links.

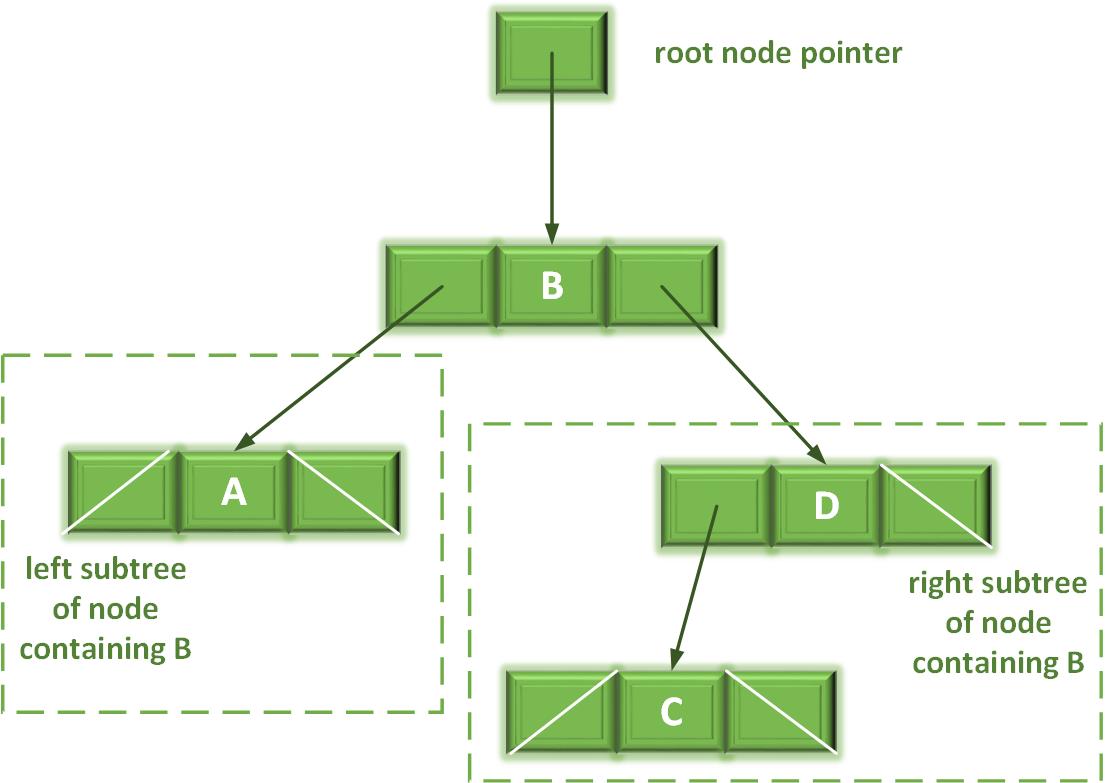
  • The root node is the first node in a tree.
  • Each link in the root node refers to a child.
  • The left child is the first node in the left subtree, and the right child is the first node in the right subtree.
  • The children of a node are called siblings.
  • A node with no children is called a leaf node.
Binary Tree in C Programming
Binary Trees in C Programming

Function insertNode

Function insertNode receives the address of the tree and an integer to be stored in the tree as arguments. A node can be inserted only as a leaf node in a binary search tree. 


    // insert node into tree
    void insertNode( TreeNodePtr *treePtr, int value ){ 
    
    // if tree is empty
    if ( *treePtr == NULL ) {   
      *treePtr = malloc( sizeof( TreeNode ) );
    
    // if memory was allocated, then assign data
      if ( *treePtr != NULL ) { 
         ( *treePtr )->data = value;
         ( *treePtr )->leftPtr = NULL;
         ( *treePtr )->rightPtr = NULL;
      } // end if
      else {
         printf( "%d not inserted. No memory available.\n", value );
      } // end else
    } // end if
    else { // tree is not empty
    
    // data to insert is less than data in current node
      if ( value < ( *treePtr )->data ) {                   
         insertNode( &( ( *treePtr )->leftPtr ), value );   
      } // end if                                        
    
    // data to insert is greater than data in current node
      else if ( value > ( *treePtr )->data ) {                 
         insertNode( &( ( *treePtr )->rightPtr ), value );     
      } // end else if                                      
      else { // duplicate data value ignored
         printf( "%s", "dup" );
      } // end else
     } // end else
    } // end function insertNode

Functions inOrder, preOrder and postOrder

The inOrder traversal of a binary search tree prints the node values in ascending order.

The steps for an inOrder traversal are:

  • Traverse the left subtree inOrder.
  • Process the value in the node.
  • Traverse the right subtree inOrder. 

    // begin inorder traversal of tree
    void inOrder( TreeNodePtr treePtr ) { 
    
    // if tree is not empty, then traverse
    if ( treePtr != NULL ) {                
      inOrder( treePtr->leftPtr );         
      printf( "%3d", treePtr->data );      
      inOrder( treePtr->rightPtr );        
    } // end if                          
    } // end function inOrder

The steps for a preOrder traversal are:

  • Process the value in the node.
  • Traverse the left subtree preOrder.
  • Traverse the right subtree preOrder. 

    // begin preorder traversal of tree
    void preOrder( TreeNodePtr treePtr ) { 
    
    // if tree is not empty, then traverse
    if ( treePtr != NULL ) {                
      printf( "%3d", treePtr->data );      
      preOrder( treePtr->leftPtr );        
      preOrder( treePtr->rightPtr );       
    } // end if                          
    } // end function preOrder

The value in each node is processed as the node is visited.

The steps for a postOrder traversal are:

  • Traverse the left subtree postOrder.
  • Traverse the right subtree postOrder.
  • Process the value in the node.

The value in each node is not printed until the values of its children are printed. 


    // begin postorder traversal of tree
    void postOrder( TreeNodePtr treePtr )
    { 
    
    // if tree is not empty, then traverse
    if ( treePtr != NULL ) {                
      postOrder( treePtr->leftPtr );       
      postOrder( treePtr->rightPtr );      
      printf( "%3d", treePtr->data );      
    } // end if                          
    } // end function postOrder
Note:

to run the program you need to buid first a main menu using the switch (choice) statement for the functions insertNode, inOrder, preOrder and postOrder.

Ads Right